Penelitian yang diinisiasi oleh Sigit Pancahayani (Dosen Program Studi Statistika Institut Teknologi Kalimantan (ITK)), Annisa Rahmita Soemarsono (Dosen Program Studi Matematika ITK), Dieky Adzkiya (Dosen Program Studi Matematika Institut Teknologi Sepuluh Nopember (ITS)), dan Musyarofah (Dosen Program Studi Fisika ITK), serta melibatkan mahasiswa Program Studi Matematika ITK, Rinda Fariasih, merupakan salah satu bentuk penelitian kerja sama antara ITK dan ITS yang dilakukan dalam kurun waktu 6-8 bulan. Topik penelitian yang diangkat dalam penelitian ini didasarkan pada permasalahan di kehidupan sehari-hari, terutama di lingkungan kerja. Ketidakseimbangan beban kerja yang dimiliki oleh masing-masing karyawan di suatu perusahaan ternyata memiliki dampak pada hasil pekerjaan. Dengan memanfaatkan salah satu konsep graf, permasalahan tersebut diharapkan dapat diminimalisir.
Dalam sebuah organisasi, beberapa masalah mungkin muncul dan terkadang membutuhkan formulasi formal untuk menemukan solusi terbaik. Formula ini biasanya ditulis dalam notasi matematika dan pemodelan. Masalah yang timbul dalam suatu instansi, seperti pemberian tugas kepada pegawai, seringkali memerlukan pertimbangan ekstra karena dapat menimbulkan beban kerja yang tidak seimbang antar pegawai. Berkaitan dengan masalah ini, beberapa peneliti telah melakukan berbagai metode seperti Linear Programming menggunakan Metode Hungarian dan penjadwalan.
Salah satu metode yang dipelajari dalam teori graf, yakni dekomposisi ajaib, juga dapat diterapkan untuk menyelesaikan masalah-masalah yang berkaitan dengan penugasan di suatu perusahaan. Dengan menggunakan metode tersebut, mula-mula alur kerja di perusahaan perlu dimodelkan sebagai graf. Misal perusahaan memiliki beberapa divisi dan untuk setiap divisi terdiri dari jumlah karyawan yang sama beserta tugasnya masing-masing. Para karyawan di divisi tersebut dilambangkan dengan titik dan tugas diilustrasikan sebagai sisi. Tujuannya adalah untuk menemukan penyusunan yang paling proporsional sehingga setiap divisi memiliki beban kerja yang sama.
Untuk mengimplementasikan konsep tersebut, digunakan notasi teori graf sebagai berikut. Misal G=V,E merupakan graf berhingga, sederhana, dan terhubung dengan himpunan titik V dan himpunan sisi E. G dikatakan graf yang dapat didekomposisi jika terdapat himpunan subgraf dari G, misal H=Hi1≤i≤n} sedemikian hingga untuk setiap i≠j, Hi isomorfis terhadap Hj, i=1nHi=G dan memenuhi EHi∩EHj=∅ jika i≠j.
Misal f:VG∪EG→{1,2,…, VG+E(G)} adalah pemetaan bijektif sedemikian hingga untuk setiap subgraf di dalam H memiliki bobot yang sama, dinotasikan dengan w, artinya untuk v∈V(Hi) dan e∈EG keduanya menghasilkan wHi=∑fv+fe=k. Di dalam penelitian ini, notasi k disebut konstanta ajaib. Jika setiap subgraf Hi≅H dari G memenuhi pelabelan tersebut, maka G dapat dikatakan sebagai dekomposisi ajaib dari graf H. Sebaliknya, jika bobot total dari semua subgraf berbeda, maka G dikatakan sebagai dekomposisi anti ajaib dari graf H.
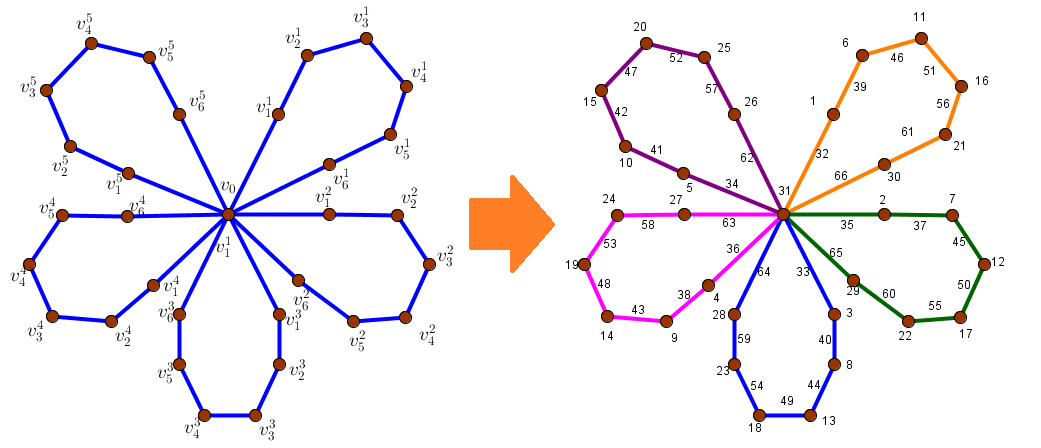
Penelitian ini membahas tentang dekomposisi ajaib dan anti ajaib dari siklus amalgamasi titik. Didefinisikan amalgamasi AmalCnt dari banyaknya siklus t dengan orde n di dalam C={Ci| 1≤i≤n} yang dikonstruksi dengan menggabungkan semua Ci di dalam titik v0 yang dinamakan titik terminal. Untuk memperoleh dekomposisi yang diinginkan, perlu didefinisikan label titik label sisi di dalam graf tersebut.
Dari penelitian ini, didapatkan hasil yang dinyatakan dalam teorema, yaitu
Teorema 1
Untuk n yang meupakan bilangan positif dan t adalah bilangan asli maka graf amalgamasi dapat didekomposisi ke dalam t buah siklus yang bersifat ajaib dan anti ajaib.
Selain itu, nilai konstanta ajaib dari masing-masing subgraf juga dapat ditentukan secara beragam dan memiliki suatu rentang berdasarkan batas bawah dan batas atas.
Dari teorema tersebut, dapat dikonstruksi contoh susunan beban kerja pegawa yang direpresentasikanoleh gabungan lima buah graf siklus berorder 7.
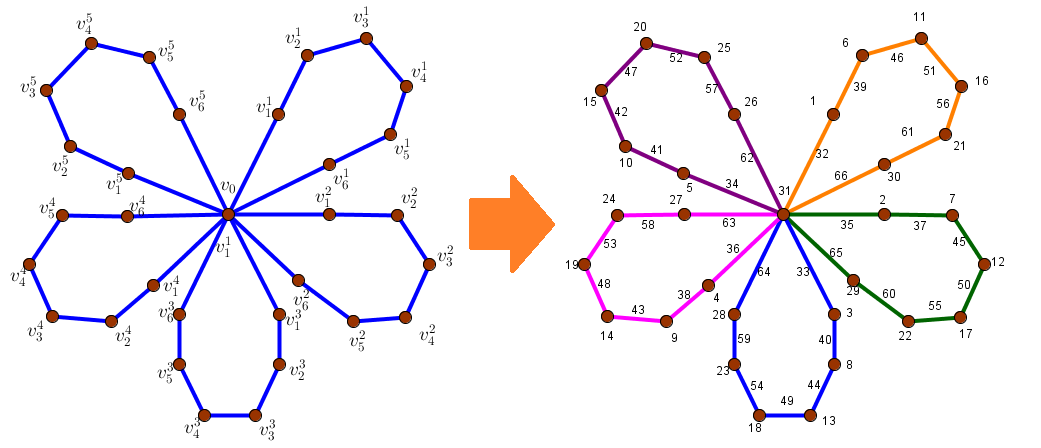
Gambar 1. Pelabelan titik dan sisi pada amalgamasi 5 siklus berorde 7
Berdasarkan penelitian yang telah dilakukan dan hasil yang diperoleh, dapat disimpulkan bahwa dapat dikonstruksi beberapa aturan yang direpresentasikan oleh Teorema 1 sebagai salah satu alternatif penyelesaian dalam masalah optimasi beban kerja karyawan di perusahaan.